中文  |  English
天然气勘探与开发

天然气勘探与开发 >

2025 , Vol. 48 >Issue 2: 103 - 112

DOI: https://doi.org/10.12055/gaskk.issn.1673-3177.2025.02.010

油气田开发

海上薄互层油藏反向压驱压裂施工压力预测方法

  • 段宝江 ,
  • 李建荣 ,
  • 王一超 ,
  • 蔡振华 ,
  • 李奇 ,
  • 钱继贺
展开
  • 中海油能源发展股份有限公司工程技术分公司 天津塘沽 300452

段宝江，男，1987年生，硕士，高级工程师；主要从事油气田开发研究工作。地址：（300452）天津市塘沽区东沽石油新村三区105-704。E-mail：

Copy editor: 佘娟

收稿日期: 2024-10-11

  修回日期: 2025-02-25

  网络出版日期: 2025-04-30

基金资助

中海油能源发展股份有限公司重大专项(HFKJ-ZX-GJ-2023-02)

中国海洋石油集团有限公司“十四五”重大科技项目(KJGG2022-0704)

收起

Operation pressure prediction of reverse pressure drive and fracturing for offshore thin interbedded reservoirs

  • DUAN Baojiang ,
  • LI Jianrong ,
  • WANG Yichao ,
  • CAI Zhenhua ,
  • LI Qi ,
  • QIAN Jihe
Expand
  • EnerTech-Drilling & Production Co., China National Offshore Oil Corporation, Tianjin 300452, China

Received date: 2024-10-11

  Revised date: 2025-02-25

  Online published: 2025-04-30

Fold

摘要

为了破解南海西部某低渗透薄互层油藏钻井资料少、非均质性强、地层能量亏空严重等难题，进而精准预测该油藏反向压驱压裂施工压力，基于斯皮尔曼相关性和灰色关联分析等方法，结合线性回归和机器学习技术，构建了施工压力预测模型。首先，通过斯皮尔曼相关性和灰色关联分析，筛选出对裂缝延伸压力梯度影响显著的地质油藏与工程参数；其次，基于筛选出的参数，分别利用线性回归和机器学习方法建立施工压力预测模型；最后，以该区块A1井的实际数据验证模型精度。研究结果表明：①斯皮尔曼相关性和灰色关联分析方法能有效识别影响裂缝延伸压力梯度的关键参数；②线性回归和机器学习方法的预测偏差率均在10%以内，可以满足工程精度要求；③在使用高黏液体压裂时，机器学习方法的预测精度显著优于线性回归方法；④A1井的压驱与压裂施工压力预测值与实际值高度吻合，验证了所建模型的可靠性。结论认为，基于机器学习的施工压力预测方法能够为南海西部低渗透薄互层油藏的反向压驱压裂作业提供精准指导，同时也可以为其他类似储层改造作业的压力预测提供参考。

关键词： 低渗透薄互层油藏; 反向压驱压裂; 裂缝延伸压力; 灰色关联; 机器学习

本文引用格式

段宝江 , 李建荣 , 王一超 , 蔡振华 , 李奇 , 钱继贺 . 海上薄互层油藏反向压驱压裂施工压力预测方法[J]. 天然气勘探与开发, 2025 , 48(2) : 103 -112 . DOI: 10.12055/gaskk.issn.1673-3177.2025.02.010

Abstract

In order to address the challenges of limited drilling data, strong heterogeneity, and severe formation energy voidage in a low-permeability thin interbedded oil reservoir in the western South China Sea, and then to accurately predict the pressure during reverse pressure drive and fracturing operations in this reservoir, operation pressure prediction models were developed based on the Spearman correlation and grey relational analysis (GRA), together with linear regression and machine learning technologies. Firstly, geological reservoir and engineering parameters that significantly affect the pressure gradient of fracture extension were screened out through Spearman correlation and GRA. Secondly, based on the selected parameters, operation pressure prediction models were established by using linear regression and machine learning methods. Finally, these models were validated using the actual data from Well A1 in the reservoir. The results indicate that, (i) the methods of Spearman correlation and GRA can effectively identify key parameters affecting the pressure gradient of fracture extension; (ii) the prediction deviation rates of both linear regression and machine learning are within 10%, meeting the required engineering accuracy; (iii) when high-viscosity fracturing fluids are used, the prediction accuracy of machine learning is much superior to that of linear regression; and (iv) the predicted values of operation pressure in pressure drive and fracturing are highly consistent with the actual ones in Well A1, validating the reliability of the established models. The conclusion suggests that the operation pressure prediction method based on machine learning can provide an accurate guidance for reverse pressure drive and fracturing operations in the low-permeability thin interbedded reservoir in the western South China Sea. Additionally, it can serve as a reference for pressure prediction in similar reservoir stimulation operations.

Key words： Low-permeability thin interbedded oil reservoir; Reverse pressure drive and fracturing; Fracture extension pressure; Grey relation; Machine learning

0 引言

南海西部W油田作为海上第一个整装开发低渗透油田，由于储层物性差和非均质性严重，部分井组存在注采连通性差、注水收效差，造成地层能量低、产能递减快的问题。通过大规模反向压驱压裂的方式对油井进行增产改造，取得了较好的效果[1-3]。
反向压驱工艺首先通过在采出井高排量注入高滤失表活剂，使表活剂通过动态裂缝快速进入储层基质，其次利用大规模加砂压裂建立高导流裂缝，最后通过焖井渗吸，让药剂充分乳化发挥洗油作用[4-9]。
但是，在前期压驱压裂施工过程中，发现在反向压驱和压裂阶段，井口施工压力差异较大，裂缝延伸压力实际值与设计预测偏差较大。造成这种现象的原因主要有以下几个方面：①大多数目标井本身没有声波测井，对地应力的计算更多来自经验公式；②施工井均为亏空井，地层最小水平主应力已经随着生产发生改变；③储层纵向上具有层多、层薄，隔层效果差，由于压驱液与压裂液黏度的不同，在相同施工排量下，不同黏度的液体裂缝延伸存在不同。
目前国内对于压裂施工压力的预测，主要手段还是通过声波测井数据进行地应力分析，辅以岩石力学性能测试修正地应力计算公式[10-13]。现场施工时，一般取一个范围较为宽泛的地应力梯度值，计算结果与实际值差别较大。另一方面，对水力压裂过程中射孔孔眼摩阻和管柱沿程摩阻计算方法研究较为丰富，计算准确度良好[14-16]。
由于海上作业空间受限，设备动复原成本高，无法像陆上压裂设计作业中预留附加泵作为应急备用方案，因此对于施工水马力计算精确度要求较高，进而对施工压力的预测精准度要求较高，陆上常用的施工压力预测方式适用性欠佳。本文利用斯皮尔曼相关性[17-18]和灰色关联方法[19-22]来刻画裂缝延伸压力及地质油藏、工程各因素之间的影响程度，客观分析施工压力的影响因素。选取相关性较强的参数利用线性回归[23-26]和机器学习[27-31]的方式，以期为施工压力预测提供可靠的计算方法。

1 分析目标的确定

南海西部W油田古近系流沙港组二段为中孔低渗薄互层油藏，纵向小层数多，横向变化快，连通关系复杂；平面上，受沉积环境的影响，储层物性差异大，平面非均质性强。纵向上，呈薄互层特征，单砂体厚度薄（1.0~5.0 m）。井型一般为定向井，完井方式均采用射孔完井，孔眼直径11 mm，射孔密度30孔/m，射孔相位60°，射孔井段除非遇到连续超过20 m泥岩，一般将整个流二段砂泥薄互层全储层射开。本文选择已施工的5口井10层反向压驱压裂井作为分析对象，以反向压驱和压裂时裂缝延伸压力梯度作为目标。通过现场施工直接能够获得的数据为井口施工压力，选取注入压驱液及压裂液前置液时的施工曲线，以较为平稳处的压力作为裂缝延伸时的井口压力（图1）。
图1 裂缝延伸压力选取示意图

Fig. 1 Selection of fracture extension pressure

通过公式（1）将井口压力折算到井底。
p井底 = p井口 + p液注 - p管柱沿程摩阻
由于不同的井不同阶段施工排量不同，管柱摩阻按照公式（2）计算，该公式通过实验室与矿场验证，计算该体系压驱液与压裂液管柱摩阻较为准确，现场应用的压驱液和压裂液的降阻率均为60%。
p管柱沿程摩阻 = 1.386 6 × 1012 D-4.8 Q1.8 L
式中D表示管柱，mm；Q表示施工排量，m3/min；L表示管柱长度，m。
为了方便对比，以分析对象储层中深计算各层井底压驱梯度和压裂梯度作为分析目标，计算结果见表1。
表1 分析对象压驱压力梯度和压裂压力梯度表

Table 1 Pressure gradients of pressure drive and fracturing of the analyzed objects

井
号		 层数 层位 储层
中深/
m		 排量/
（m3·min-1）		 管柱
摩阻/
MPa		 地面压驱压力/
MPa		 地面压裂压力/
MPa		 井底压
驱压力/
MPa		 井底压
裂压力/
MPa		 井底压驱
梯度/
（MPa·m-1）		 井底压裂
梯度/
（MPa·m-1）
1 1 L2Ⅰ 2 353.90 6.00 10.36 33.00 43.00 46.89 56.89 0.019 9 0.024 2
2 L2Ⅱ 2 427.70 6.00 10.58 21.00 27.00 44.43 41.43 0.018 3 0.017 1
2 1 L2Ⅱa 2 521.36 4.40 12.78 45.00 43.00 58.19 59.19 0.023 1 0.023 5
2 L2Ⅱb 2 561.97 5.00 16.47 45.00 48.00 54.92 55.00 0.021 4 0.021 5
3 1 L2Ⅱa 2 228.48 6.00 11.69 36.00 40.00 47.26 51.26 0.021 2 0.023 0
2 L2Ⅱb 2 275.15 6.00 11.66 36.00 38.00 47.77 49.77 0.021 0 0.021 9
3 L2Ⅱc 2 321.65 6.00 11.96 40.00 40.50 51.95 52.45 0.022 4 0.022 6
4 1 L2Ⅱa+b 2 560.82 5.00 10.61 34.00 37.00 50.00 52.77 0.019 5 0.020 6
2 L2Ⅱc 2 617.81 5.00 9.03 32.00 38.00 51.00 55.93 0.019 5 0.021 4
5 1 L2Ⅱa+b+c 2 184.96 6.00 10.00 22.11 28.00 42.00 44.00 0.019 2 0.020 1

2 影响因素关联度及权重的确定

影响因素关联度的数据分析方法主要有相关系数分析法、灰色关联分析法。前者简单直观、适用广泛，但分析结果容易受到数据异常值影响，导致结果偏差；后者虽然存在主观性强、适用范围有限等问题，但该方法对数据样本量要求低、计算简便，是工程上常用的数据分析方法。

2.1 数据处理

根据分析目标的资料，考虑地层影响因素有：储层斜厚（M1）、储层垂厚（M2）、油层数量（M3）、油层厚度（M4）、泥岩层厚度（M5）、储层平均GR值（M6）、砂岩平均GR值（M7）、地层倾角（M8）。考虑工程影响因素有：储层射孔处井斜角（M9）、总射孔数量（M10）、施工排量（M11）。
以影响压驱裂缝延伸压力梯度和压裂裂缝延伸压力梯度因素为指标，其测试值序列为：
$\left\{ {{X}_{i}}(j) \right\}=\left\{ {{X}_{0}}(1),{{X}_{1}}(2),\cdot \cdot \cdot,{{X}_{m}}(n) \right\}$
式中${{X}_{i}}(j)$表示$m\times n$维矩阵；i表示评价井层数；j为评价指标数。
为使目标因素和影响因素具有可比性，对其无因次化处理，处理方法为平均法，即
${{Y}_{i}}(j)=\frac{{{x}_{i}}(j)}{\frac{1}{m}\sum\nolimits_{j=1}^{m}{{{x}_{i}}(j)}}$
式中${{Y}_{i}}(j)$表示$m\times n$维矩阵的无因次。
处理结果如表2所示。
表2 目标因素和影响因素无因次化处理结果表

Table 2 Dimensionless processing results of target factors and influencing factors

目标因素 影响因素
压驱压力
梯度		 压裂压力
梯度		 M1 M2 M3 M4 M5 M6 M7 M8 M9 M10 M11
0.968 1.121 0.472 0.558 0.723 0.451 0.713 0.927 1.029 0.970 0.655 0.675 1.083
0.891 0.792 1.424 1.686 1.566 1.803 1.759 1.008 1.167 0.970 0.655 1.232 1.083
1.124 1.089 0.576 0.411 1.446 0.518 0.295 0.870 0.954 1.370 1.388 0.821 0.794
1.041 0.996 1.294 0.926 1.687 0.778 0.999 0.847 0.941 1.370 1.388 1.150 0.903
1.032 1.065 0.535 0.489 0.602 0.704 0.171 1.113 1.079 1.142 1.120 0.739 1.083
1.022 1.014 1.133 1.034 0.843 1.239 0.761 1.030 1.029 1.142 1.120 1.006 1.083
1.090 1.047 0.772 0.708 0.482 0.817 0.480 0.883 0.966 1.142 1.120 0.821 1.083
0.949 0.954 1.246 1.264 0.843 1.268 1.370 1.221 1.004 1.027 0.974 1.134 0.903
0.949 0.991 0.747 0.758 0.241 0.732 0.704 1.093 0.903 1.027 0.974 0.698 0.903
0.934 0.931 1.801 2.166 1.566 1.690 2.749 1.008 0.929 1.142 0.609 1.724 1.083

2.2 斯皮尔曼相关系数法

斯皮尔曼相关系数法（Spearman Correlation Coefficient法，简称SCC法）用于衡量和定量评价两两变量之间的相关性，可考虑离散型变量，当变量中至少存在一个离散变量时，优先使用Spearman系数来描述两变量的相关性。将每个因素值标准化后，通过Spearman相关性量化分析发现（表3），压驱压力梯度只与储层射孔处井斜角正相关，压裂压力梯度与砂岩平均GR值和储层射孔处井斜角正相关。按照影响压驱压力梯度Spearman相关系数绝对值大小排名前5位为：储层射孔处井斜角>储层垂厚>泥岩层厚度>油层厚度>地层倾角；影响压裂压力梯度Spearman相关系数绝对值大小排名前5位为：储层垂厚>油层厚度>储层斜厚>泥岩层厚度>总射孔数量。
表3 斯皮尔曼相关系数计算结果表

Table 3 Calculation results of Spearman correlation coefficients

名称 压驱
梯度		 压裂
梯度		 M1 M2 M3 M4 M5 M6 M7 M8 M9 M10 M11
压驱梯度 1.00 0.75 -0.50 -0.77 -0.15 -0.61 -0.74 -0.52 -0.12 -0.55 0.88 -0.37 -0.31
压裂梯度 0.75 1.00 -0.88 -0.90 -0.40 -0.89 -0.79 -0.32 0.14 -0.44 0.48 -0.76 -0.03
M1 -0.50 -0.88 1.00 0.90 0.68 0.90 0.85 -0.04 -0.18 0.29 -0.28 0.95 0.07
M2 -0.77 -0.90 0.90 1.00 0.48 0.92 0.94 0.26 -0.05 0.37 -0.58 0.80 0.25
M3 -0.15 -0.40 0.68 0.48 1.00 0.42 0.65 -0.42 0.00 0.20 0.02 0.81 -0.14
M4 -0.61 -0.89 0.90 0.92 0.42 1.00 0.78 0.26 0.09 0.10 -0.41 0.84 0.28
M5 -0.74 -0.79 0.85 0.94 0.65 0.78 1.00 0.06 -0.06 0.50 -0.59 0.79 0.16
M6 -0.52 -0.32 -0.04 0.26 -0.42 0.26 0.06 1.00 0.26 -0.16 -0.38 -0.10 0.16
M7 -0.12 0.14 -0.18 -0.05 0.00 0.09 -0.06 0.26 1.00 -0.49 -0.10 -0.05 0.54
M8 -0.55 -0.44 0.29 0.37 0.20 0.10 0.50 -0.16 -0.49 1.00 -0.50 0.11 -0.25
M9 0.88 0.48 -0.28 -0.58 0.02 -0.41 -0.59 -0.38 -0.10 -0.50 1.00 -0.17 -0.50
M10 -0.37 -0.76 0.95 0.80 0.81 0.84 0.79 -0.10 -0.05 0.11 -0.17 1.00 0.06
M11 -0.31 -0.03 0.07 0.25 -0.14 0.28 0.16 0.16 0.54 -0.25 -0.50 0.06 1.00

2.3 灰色关联分析法

对于数列在存在重复值的情况下，使用斯皮尔曼相关系数法有可能导致评估不准确，由于影响因素中尤其是工程因素，重复值较多，因此需要选取另一种方法进行评估。
灰色系统理论通过明确系统中各因素间主要关系，找出最大影响因素，从而分析关联度。若两因素在系统发展过程中相对变化一致，则两者关联度大；反之则两者关联度小。关联分析首先确定参考序列，然后比较其他数列同参考数列的接近程度，比较判断其他数列。
计算Yi(j)对Y0(j)在第j个点的关联度：
$\begin{align} & \xi (j)= \\ & \ \ \frac{\underset{i}{\mathop \min }\,\underset{j}{\mathop \min }\,\left| {{Y}_{0}}(j)-{{Y}_{i}}(j) \right|+0.5\underset{i}{\mathop \max }\,\underset{j}{\mathop \max }\,\left| {{Y}_{0}}(j)-{{Y}_{i}}(j) \right|}{\left| {{Y}_{0}}(j)-{{Y}_{i}}(j) \right|+\underset{i}{\mathop 0.5\max }\,\underset{j}{\mathop \max }\,\left| {{Y}_{0}}(j)-{{Y}_{i}}(j) \right|} \\ \end{align}$
式中$\xi (j)$为关联度，无因次。
计算与压驱压力梯度关联度时，目标函数压驱压力梯度就是${{Y}_{0}}(j)$，计算与压裂压力梯度关联度时，目标函数压驱压力梯度就是${{Y}_{0}}(j)$。
各个影响因素的关联度计算方式为：
${{r}_{0i}}=\frac{1}{m}\sum\nolimits_{j=1}^{m}{{{\xi }_{0i}}}(j)$ $(i=1,2,3\cdots m)$
权重系数$a_{i}$计算公式为：
${{a}_{i}}=\frac{{{r}_{0i}}}{\sum\nolimits_{i=1}^{n}{{{r}_{0i}}}}$
计算结果见表4。
表4 灰色关联分析法计算结果表

Table 4 GRA calculation results

名称 影响因素 M1 M2 M3 M4 M5 M6 M7 M8 M9 M10 M11
压驱压力
梯度		 相关性 0.702 0 0.716 4 0.685 9 0.7135 0.663 5 0.943 3 0.923 3 0.861 7 0.812 0 0.799 4 0.796 4
权重 8.15% 8.31% 7.96% 8.28% 7.70% 10.95% 10.71% 10.00% 9.42% 9.28% 9.24%
压裂压力
梯度		 相关性 0.708 2 0.664 1 0.642 0 0.675 4 0.607 5 0.861 1 0.866 7 0.892 6 0.829 0 0.773 8 0.782 6
权重 8.53% 8.00% 7.73% 8.13% 7.32% 10.37% 10.44% 10.75% 9.98% 9.32% 9.43%
按照影响压驱压力梯度灰色相关系数绝对值大小排名前5位为：砂岩平均GR值>储层平均GR值>地层倾角>射孔处井斜角>施工排量；影响压裂压力梯度灰色相关系数绝对值大小排名前5位为：地层倾角>储层平均GR值>砂岩平均GR值>射孔处井斜角>施工排量。由于压驱液体和压裂液体的黏度不同，在裂缝延伸时的净压力不同，造成影响主控因素也不相同，提示在做反向压裂压驱设计时，重点关注和优化这方面问题。

3 压驱压裂施工压力预测

3.1 线性回归（最小二乘法）

最小二乘法是多元回归分析中最常用的方法，该方法计算简单直接，属于非迭代法。线性回归主要用于研究自变量与因变量之间的线性关系。由于自变量过多，多元回归计算量太大。为了减少计算量，根据上节压驱压裂裂缝延伸压力主控因素影响权重，综合考虑权重排名前四位的砂岩平均GR值、储层平均GR值、地层倾角、射孔处井斜角作为自变量。建立了适用于本区域的压驱压裂裂缝延伸压力梯度多项式计算公式，计算系数见表5，通过表5系数计算的结果与实际值的对比以及偏差率分别见表6、图2、表7、图3。
表5 压驱压裂裂缝延伸压力梯度多项式计算系数表

Table 5 Multinomial coefficients for calculating pressure gradient of fracture extension in pressure drive and fracturing

变量 单位 压驱压力梯度计算系数 压裂压力梯度计算系数
常数 0.022 198 2 0.039 773 0
储层平均GR值（M6） API -0.000 034 9 -0.000 045 9
砂岩平均GR值（M7） API -0.000 007 5 -0.000 105 1
地层倾角（M8） （°） -0.000 083 8 -0.000 902 3
井斜角（M9） （°） 0.000 099 9 0.000 117 4
表6 线性回归计算结果与实际值对比表（压驱压力梯度）

Table 6 Comparison of linear regression calculation results with actual values (pressure gradient in pressure drive)

井名 well1-1 well1-2 well2-1 well2-2 well3-1 well3-2 well3-3 well4-1 well4-2 well5-1
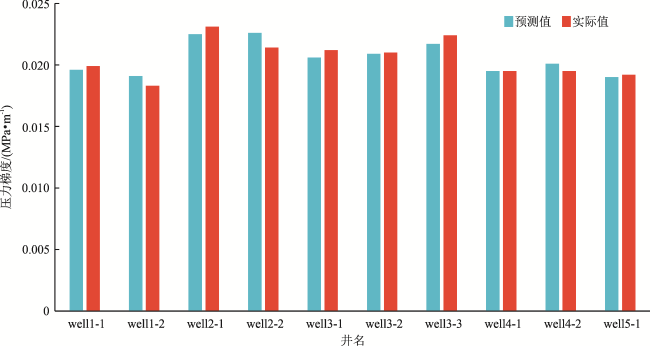
预测结果/（MPa·m-1） 0.019 5 0.019 1 0.022 6 0.022 7 0.020 5 0.020 9 0.021 6 0.019 6 0.020 2 0.018 9
实际值/（MPa·m-1） 0.019 9 0.018 3 0.023 1 0.021 4 0.021 2 0.021 0 0.022 4 0.019 5 0.019 5 0.019 2
偏差率 2% -4% 2% -6% 3% 0 4% -1% -4% 2%
图2 线性回归计算结果与实际值对比图（压驱压力梯度）

Fig. 2 Comparison of linear regression calculation results with actual values (pressure gradient in pressure drive)

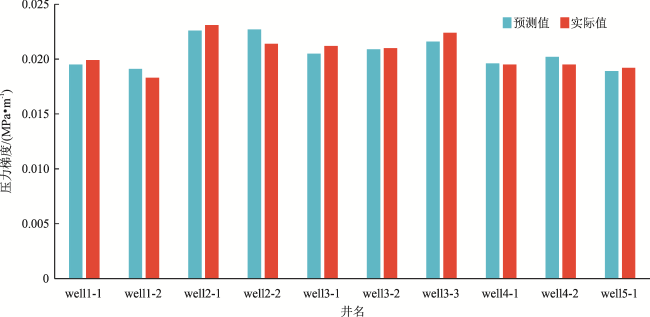
表7 线性回归计算结果与实际值对比表（压裂压力梯度）

Table 7 Comparison of linear regression calculation results with actual values (pressure gradient in fracturing)

井名 well1-1 well1-2 well2-1 well2-2 well3-1 well3-2 well3-3 well4-1 well4-2 well5-1
预测结果/（MPa·m-1） 0.021 4 0.018 7 0.022 7 0.022 9 0.020 8 0.021 7 0.023 0 0.021 0 0.022 6 0.020 2
实际值/（MPa·m-1） 0.024 2 0.017 1 0.023 5 0.021 5 0.023 0 0.021 9 0.022 6 0.020 6 0.021 4 0.020 1
偏差率 12% -10% 3% -7% 10% 1% -2% -2% -5% 0
图3 线性回归计算结果与实际值对比图（压裂压力梯度）

Fig. 3 Comparison of linear regression calculation results with actual values (pressure gradient in fracturing)

3.2 机器学习回归（梯度下降法）

与最小二乘法相比，梯度下降法在特征较大时，也可以计算，而最小二乘法的时间复杂度会很大，计算精度也受影响；而梯度下降适用性极强，一般只要是凸函数，都可以通过梯度下降法得到全局最优值。
一元线性回归方程为：
$y={{\beta }_{0}}+{{\beta }_{1}}x$
给定一组样本观测值xi，yi，要求回归函数尽可能拟合这组值。通过梯度下降法，将最小二乘法求取损失函数最小值问题改为代价函数：
$J({{\beta }_{0}},\ {{\beta }_{1}})=\frac{1}{2m}\sum\nolimits_{i=1}^{m}{{{({{y}_{i}}-{{x}_{i}})}^{2}}}$
式中m为数据个数，分母上的2是为了抵消求导后的系数。
梯度下降法主要步骤如下：
1 ）给定待优化连续可微代价函数J、学习率α及${{\beta }_{0}}$、${{\beta }_{1}}$初始值；
2 ）计算待优化函数梯度；
${{\beta }_{0}}:={{\beta }_{0}}-\alpha \frac{\partial J({{\beta }_{0}},{{\beta }_{1}})}{\partial {{\beta }_{0}}};\ {{\beta }_{1}}:\ ={{\beta }_{1}}-\alpha \frac{\partial J({{\beta }_{0}},\ {{\beta }_{1}})}{\partial {{\beta }_{1}}}$
3 ）更新迭代公式；
4 ）计算该处的函数梯度$\nabla J{{\beta }_{0}},{{\beta }_{1}}$；
5 ）计算梯度向量的模判断是否收敛：$\left\| \nabla J \right\|\le \varepsilon $；
6 ）若收敛，则停止，若不收敛，则从第（3）步开始迭代直到收敛。
为了与3.3节方法计算结果作对比，同样综合考虑权重排名前四位的砂岩平均GR值、储层平均GR值、地层倾角、射孔处井斜角作为自变量通过机器学习得到本区域的压驱压裂裂缝延伸压力梯度，计算的结果与实际值的对比以及偏差率分别见图4、表8、图5、表9。与线性回归结果相比，预测的压驱裂缝延伸压力梯度准确度相当，预测的压裂裂缝延伸压力梯度准确度较为提升。
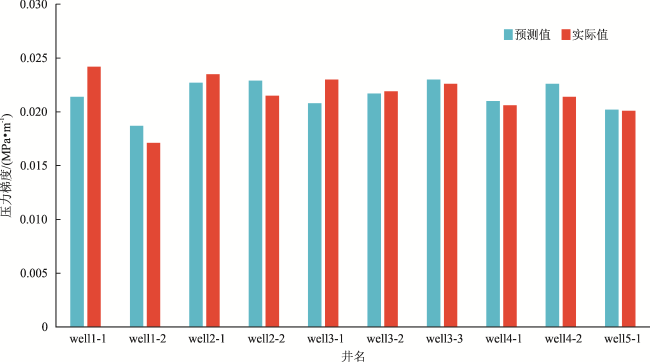
图4 机器学习回归计算结果与实际值对比图（压驱压力梯度）

Fig. 4 Comparison of machine learning regression calculation results with actual values (pressure gradient in pressure drive)

表8 机器学习回归计算结果与实际值对比表（压驱压力梯度）

Table 8 Comparison of machine learning regression calculation results with actual values (pressure gradient in pressure drive)

井名 well1-1 well1-2 well2-1 well2-2 well3-1 well3-2 well3-3 well4-1 well4-2 well5-1
预测结果/
（MPa·m-1）		 0.019 6 0.019 1 0.022 5 0.022 6 0.020 6 0.020 9 0.021 7 0.019 5 0.020 1 0.019 0
实际值/
（MPa·m-1）		 0.019 9 0.018 3 0.023 1 0.021 4 0.021 2 0.021 0 0.022 4 0.019 5 0.019 5 0.019 2
偏差率 2% -4% 3% -6% 3% 0 3% 0 -3% 1%
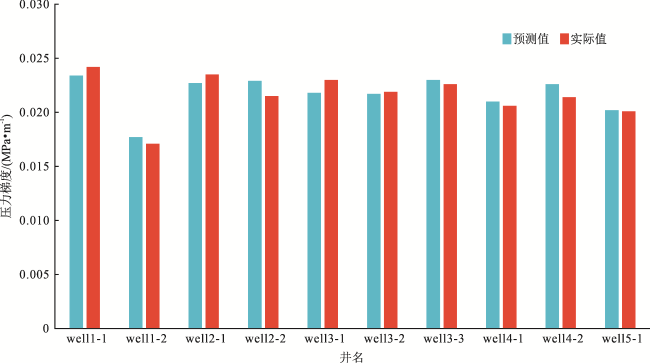
图5 机器学习回归计算结果与实际值对比图（压裂压力梯度）

Fig. 5 Comparison of machine learning regression calculation results with actual values (pressure gradient in fracturing)

表9 机器学习回归计算结果与实际值对比表（压裂压力梯度）

Table 9 Comparison of machine learning regression calculation results with actual values (pressure gradient in fracturing)

井名 well1-1 well1-2 well2-1 well2-2 well3-1 well3-2 well3-3 well4-1 well4-2 well5-1
预测结果/（MPa·m-1） 0.023 4 0.017 7 0.022 7 0.022 9 0.021 8 0.021 7 0.023 0 0.021 0 0.022 6 0.020 2
实际值/（MPa·m-1） 0.024 2 0.017 1 0.023 5 0.021 5 0.023 0 0.021 9 0.022 6 0.020 6 0.021 4 0.020 1
偏差率 3% -4% 3% -7% 5% 1% -2% -2% -5% 0

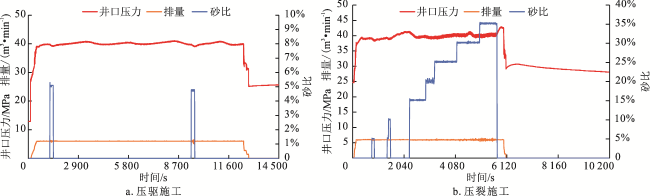
4 应用实例

A1井是同区块另一平台实施的一口反向压驱压裂井，该井采用Ø114.3 mm内径100 mm油管压裂，长度3 033 m，储层中深2 305 m，地层倾角10°、储层平均GR值120、砂岩平均GR值72、射孔处井斜角50°。通过本文第3节方法计算裂缝延伸压力梯度，通过公式（1）、（2）计算施工压力（表10）。
表10 A1井压力梯度与施工压力预测表

Table 10 Predicted values of pressure gradient and operation pressure for Well A1

名称 压驱压力梯度/（MPa·m-1） 压裂压力梯度/（MPa·m-1） 压驱施工压力/MPa 压裂施工压力/MPa
线性回归 0.021 63 0.023 54 37.21 40.50
机器学习 0.022 18 0.023 06 38.47 41.61
该井施工曲线如图6，反向压驱施工压力40.90 MPa，压裂前置液阶段施工压力41.50 MPa。
图6 A1井压驱、压裂施工曲线图

Fig. 6 Pressure drive and fracturing operation curves of Well A1

两种方法对A1井压驱和压裂施工压力的预测值与实际施工值的偏差在10%以内（表11）。
表11 两种方法预测压驱和压裂施工压力值对比表

Table 11 Predicted values of operation pressure in pressure drive and fracturing by two methods

方法类型 线性回归 机器学习
预测值/MPa 37.21 38.47
实际值/MPa 40.9 40.90
偏差值/MPa 3.69 2.43
偏差率 9.02% 5.94%

5 结论

1 ）通过灰色关联分析法分析了地质和工程因素对压驱和压裂时裂缝延伸压力梯度的影响程度，明确了排名靠前的主控因素为：地层倾角、储层平均GR值、砂岩平均GR值、射孔处井斜角。
2 ）分别通过选取相关程度较强的主控因素使用线性回归和机器学习的方式建立了施工压力预测方法，通过两种方法的对比，机器学习得到的偏差率准确度较高一些。
3 ）鉴于海上油田开发单井测井资料少的现状，通过数理统计的方法预测压驱压裂施工压力，丰富了施工压力计算方法，通过A1井实际施工对该方法进行了验证，预测值与实际值较为接近，对后期本区域反向压驱压裂施工参数的选择提供了可靠的帮助和指导。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
段宝江, 王一超, 钱继贺, 等. 海上低渗薄互层反向压驱压裂工艺技术研究及应用[J]. 复杂油气藏, 2024, 17(3): 362-366.

DUAN Baojiang, WANG Yichao, QIAN Jihe, et al. Research and application of reverse injection fracturing technology for offshore low-permeability thin interbedded reservoirs[J]. Complex Hydrocarbon Reservoirs, 2024, 17(3): 362-366.

[2]
吴忠宝, 李莉, 阎逸群. 超低渗油藏体积压裂与渗吸采油开发新模式[J]. 断块油气田, 2019, 26(4): 491-494.

WU Zhongbao, LI Li, YAN Yiqun. New development pattern of network fracturing and imbibition oil recovery for super-low permeability oil reservoirs[J]. Fault-Block Oil & Gas Field, 2019, 26(4): 491-494.

[3]
钟森, 赵祚培, 王淑静, 等. 低品位砂岩气藏压裂技术研究及应用——以DF109H井为例[J]. 天然气技术与经济, 2024, 18(4): 32-36.

DOI

ZHONG Sen, ZHAO Zuopei, WANG Shujing, et al. Fracturing technologies for low-grade sandstone gas reservoirs and their application to DF109H well[J]. Natural Gas Technology and Economy, 2024, 18(4): 32-36.

[4]
郭建春, 马莅, 卢聪. 中国致密油藏压裂驱油技术进展及发展方向[J]. 石油学报, 2022, 43(12): 1788-1797.

DOI

GUO Jianchun, MA Li, LU Cong. Progress and development directions of fracturing flooding technology for tight reservoirs in China[J]. Acta Petrolei Sinica, 2022, 43(12): 1788-1797.

DOI

[5]
李扬成, 汪玉梅, 杨光. 论压裂驱油技术在大庆油田的应用[J]. 中国石油和化工标准与质量, 2017, 37(23): 163-164.

LI Yangcheng, WANG Yumei, YANG Guang. Application of fracturing oil displacement technology in Daqing oilfield[J]. China Petroleum and Chemical Standard and Quality, 2017, 37(23): 163-164.

[6]
何金钢, 王洪卫. 三类油层压裂驱油技术设计及效果研究[J]. 西南石油大学学报(自然科学版), 2018, 40(5): 95-104.

DOI

HE Jingang, WANG Hongwei. Design and effect of fracture-flooding in Class Ⅲ oil reservoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2018, 40(5): 95-104.

[7]
马玉娟. 大庆长垣油田三类油层压裂驱油提高采收率技术及其应用[J]. 大庆石油地质与开发, 2021, 40(2): 103-109.

MA Yujuan. Application of fracturing-flooding EOR technique in Type Ⅲ oil reservoirs in Daqing Placanticline Oilfield[J]. Petroleum Geology & Oilfield Development in Daqing, 2021, 40(2): 103-109.

[8]
白晓虎, 齐银, 何善斌, 等. 致密储层水平井压裂-补能-驱油一体化重复改造技术[J]. 断块油气田, 2021, 28(1): 63-67.

BAI Xiaohu, QI Yin, HE Shanbin, et al. Integrated re-stimulating technology of fracturing-replenishment- displacement of horizontal wells in tight reservoirs[J]. Fault-Block Oil & Gas Field, 2021, 28(1): 63-67.

[9]
张志坚, 黄熠泽, 闫坤, 等. 低渗透油藏渗吸采油技术进展与展望[J]. 当代化工, 2021, 50(2): 374-378.

ZHANG Zhijian, HUANG Yize, YAN Kun, et al. Development and prospect of the imbibition oil recovery technology in low permeability reservoirs[J]. Contemporary Chemical Industry, 2021, 50(2): 374-378.

[10]
李传亮, 孔祥言. 油井压裂过程中岩石破裂压力计算公式的理论研究[J]. 石油钻采工艺, 2000, 22(2): 54-56.

LI Chuanliang, KONG Xiangyan. A theoretical study on rock breakdown pressure calculation equations of fracturing process[J]. Oil Drilling & Production Technology, 2000, 22(2): 54-56.

[11]
梁何生, 刘凤霞, 张国龙, 等. 一种地层破裂压力估算方法及应用[J]. 石油钻探技术, 1999, 27(6): 14-15.

LIANG Hesheng, LIU Fengxia, ZHANG Guolong, et al. A method to estimate formation fracture pressure and its applications[J]. Petroleum Drilling Techniques, 1999, 27(6): 14-15.

[12]
黄荣樽, 庄锦江. 一种新的地层破裂压力预测方法[J]. 石油钻采工艺, 1986, 8(3): 1-14.

HUANG Rongzun, ZHUANG Jinjiang. A new method for predicting formation fracture pressure[J]. Oil Drilling & Production Technology, 1986, 8(3): 1-14.

[13]
耶格, 库克. 岩石力学基础[M]. 中国科学院工程力学研究所, 译. 北京: 科学出版社, 1981.

JAEGER J. C., COOK N. G. W.. Fundamentals of Rock Mechanics[M]. Institute of Engineering Mechanics, Chinese Academy of Sciences, trans trans. Beijing: Science Press, 1981.

[14]
郭建春, 邓燕, 赵金洲. 大位移井压裂地面施工压力预测模型研究[J]. 钻采工艺, 2005, 28(1): 50-52.

GUO Jianchun, DENG Yan, ZHAO Jinzhou. Calculation of the surface construction pressure in fracturing the extended reach wells[J]. Drilling & Production Technology, 2005, 28(1): 50-52.

[15]
刘合, 张广明, 张劲, 等. 油井水力压裂摩阻计算和井口压力预测[J]. 岩石力学与工程学报, 2010, 29(增刊1): 2833-2839.

LIU He, ZHANG Guangming, ZHANG Jin, et al. Friction loss calculation and surface pressure prediction in oil well hydraulic fracturing[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 2833-2839.

[16]
肖雯. 径向井压裂技术携砂液摩阻影响参数研究[J]. 复杂油气藏, 2019, 12(4): 71-75.

XIAO Wen. Study on influencing parameters of sand-carrying fluid friction in radial well fracturing[J]. Complex Hydrocarbon Reservoirs, 2019, 12(4): 71-75.

[17]
SPEARMAN C.. The proof and measurement of association between two things[J]. The American Journal of Psychology, 1904, 15(1): 72-101.

[18]
肖阳, 王家豪, 李志刚, 等. 基于大数据的页岩油区块产量差异分析方法研究[J]. 钻采工艺, 2022, 45(3): 73-78.

XIAO Yang, WANG Jiahao, LI Zhigang, et al. Study on production difference analysis method of shale oil play based on big data[J]. Drilling & Production Technology, 2022, 45(3): 73-78.

[19]
易地生, 郭萍. 灰色理论与方法[M]. 北京: 石油工业出版社, 1992.

YI Disheng, GUO Ping. Grey Theory and Methods[M]. Beijing: Petroleum Industry Press, 1992.

[20]
王坤杰. 灰色关联法在储层改造效果因素分析中的应用[J]. 油气井测试, 2023, 32(6): 29-33.

WANG Kunjie. Application of gray correlation method in the analysis of reservoir transformation effect factors[J]. Well Testing, 2023, 32(6): 29-33.

[21]
程汉列, 王连山, 李林, 等. 灰色关联法分析塔中油气藏开发效果影响因素[J]. 中外能源, 2016, 21(11): 44-47.

CHENG Hanlie, WANG Lianshan, LI Lin, et al. Analysis on the influencing factors of oil and gas reservoir development in Tazhong area by gray correlation method[J]. Sino-Global Energy, 2016, 21(11): 44-47.

[22]
岳雨晴. 致密储层可压性评价方法及其评价效果试验考察[D]. 重庆: 重庆大学, 2019.

YUE Yuqing. Method for fracability evaluation of tight reservoirs and verification of its validation through experiments[D]. Chongqing: Chongqing University, 2019.

[23]
任雪松, 于秀林. 多元统计分析(第二版)[M]. 北京: 中国统计出版社, 2011.

REN Xuesong, YU Xiulin. Multivariate Statistical Analysis (Second Edition)[M]. Beijing: China Statistics Press, 2011.

[24]
刘文祎, 王涛. 基于多元线性回归的页岩油储层压裂效果预测方法研究[J]. 石化技术, 2024, 31(6): 251-254.

LIU Wenyi, WANG Tao. A prediction method of shale oil reservoir fracturing effect based on multiple linear regression[J]. Petrochemical Industry Technology, 2024, 31(6): 251-254.

[25]
孙翰文, 费繁旭, 高阳, 等. 吉木萨尔陆相页岩水平井压裂后产量影响因素分析[J]. 特种油气藏, 2020, 27(2): 108-114.

SUN Hanwen, FEI Fanxu, GAO Yang, et al. Production sensitivity analysis of fractured horizontal wells in Jimusar continental shale[J]. Special Oil & Gas Reservoirs, 2020, 27(2): 108-114.

[26]
KUO Y., YANG T., HUANG G. W.. The use of grey relational analysis in solving multiple attribute decision- making problems[J]. Computers & Industrial Engineering, 2008, 55(1): 80-93.

[27]
DAS H., ROUT J. K., MOHARANA S. C., et al. Applied Intelligent Decision Making in Machine Learning[M]. Boca Raton: CRC Press, 2020.

[28]
刘巍, 刘威, 谷建伟. 基于机器学习方法的油井日产油量预测[J]. 石油钻采工艺, 2020, 42(1): 70-75.

LIU Wei, LIU Wei, GU Jianwei. Oil production prediction based on a machine learning method[J]. Oil Drilling & Production Technology, 2020, 42(1): 70-75.

[29]
谢坤, 吴湛奇, 李彦阅, 等. 机器学习在油气开发领域的应用及展望[J]. 西安石油大学学报(自然科学版), 2023, 38(5): 58-67.

XIE Kun, WU Zhanqi, LI Yanyue, et al. Application of machine learning in oil and gas development field and its prospect[J]. Journal of Xi’an Shiyou University (Natural Science Edition), 2023, 38(5): 58-67.

[30]
郭子熙, 马骉, 张帅, 等. 深度学习在油气产量预测中的研究进展与技术展望[J]. 天然气工业, 2024, 44(9): 88-98.

GUO Zixi, MA Biao, ZHANG Shuai, et al. Research status and prospects of deep learning in oil and gas production prediction[J]. Natural Gas Industry, 2024, 44(9): 88-98.

[31]
魏漪, 赵国玺, 周雯鸽, 等. 模糊数学方法在长庆油田低渗透储层综合评价中的应用[J]. 石油天然气学报, 2011, 33(1): 60-62.

WEI Yi, ZHAO Guoxi, ZHOU Wenge, et al. The Application of fuzzy mathematic method in comprehensive evaluation for the low permeability reservoirs of Changqing Oilfield[J]. Journal of Oil and Gas Technology, 2011, 33(1): 60-62.

Options
文章导航

/

〈 〉

地址：成都市高新区天府大道北段12号
邮编：610041
电话：（028）86015441、86015319、86015549
E-mail：trqktykf@gaskk.com
技术支持：北京玛格泰克科技发展有限公司
访问统计
网站版权 © 《天然气勘探与开发》编辑部